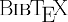Representations of groups on banach spaces

Enlaces del Item
URI: http://hdl.handle.net/10818/62751Visitar enlace: https://www.scopus.com/inward/ ...
ISSN: 29939
DOI: 10.1090/proc/16499
Compartir
Estadísticas
Ver Estadísticas de usoCatalogación bibliográfica
Mostrar el registro completo del ítemFecha
2024Resumen
We establish a general framework for representability of a metric group on a (well-behaved) class of Banach spaces. More precisely, let G be a topological group, and A a unital symmetric C∗-subalgebra of UC(G), the algebra of bounded uniformly continuous functions on G. Generalizing the notion of a stable metric, we study A-metrics δ, i.e., the function δ(e, ·) belongs to A; the case A = WAP(G), the algebra of weakly almost periodic functions on G, recovers stability. If the topology of G is induced by a left invariant metric d, we prove that A determines the topology of G if and only if d is uniformly equivalent to a left invariant A-metric. As an application, we show that the additive group of C[0, 1] is not reflexively representable; this is a new proof of Megrelishvili [Topological transformation groups: selected topics, Elsevier, 2007, Question 6.7] (the problem was already solved by Ferri and Galindo [Studia Math. 193 (2009), pp. 99–108] with different methods and later the results were generalized by Yaacov, Berenstein, and Ferri [Math. Z. 267 (2011), pp.129–138]). Let now G be a metric group, and assume A ⊆ LUC(G), the algebra of bounded left uniformly continuous functions on G, is a unital C∗algebra which is the uniform closure of coefficients of representations of G on members of F, where F is a class of Banach spaces closed under l2-direct sums. We prove that A determines the topology of G if and only if G embeds into the isometry group of a member of F, equipped with the weak operator topology. As applications, we obtain characterizations of unitary and reflexive representability. © 2024 American Mathematical Society.
Palabras clave
Ubicación
Proceedings of the American Mathematical Society Vol. 152 N° 6
Colecciones a las que pertenece
- Facultad de Ingeniería [585]